Una función y(x) se llama implícita cuando está definida de la forma F(x, y) = 0 en lugar de la habitual.
El fin de este blog, es tratar problemas de calculo diferencial para poder ayudar a personas a estudiar mas fácilmente, a través de ejercicios resueltos y vídeos con su explicación.
domingo, 19 de octubre de 2014
2.9 Funciones con dominio en los números naturales y recorrido en los números reales; las sucesiones infinitas.
Una sucesión infinita es una función cuyo dominio es el conjunto de los enteros positivos.
En este trabajo, el intervalo de una sucesión infinita será un conjunto de números reales.
Si una función f es una sucesión infinita, entonces a cada entero positivo n le corresponde un número real f(n).Estos números del intervalo de f pueden representarse al escribir:
Donde an es el n-ésimo término de la sucesión.
De acuerdo con la definición de funciones, vemos que una sucesión a1,a2,a3,...,an es igual a unasucesión b1,b2,b3,...,bnsi y solo si ak=bk para todo entero positivo k.
En este trabajo, el intervalo de una sucesión infinita será un conjunto de números reales.
Si una función f es una sucesión infinita, entonces a cada entero positivo n le corresponde un número real f(n).Estos números del intervalo de f pueden representarse al escribir:
f(1),f(2),f(3),...f(n),...
Para obtener la forma de subíndice de una sucesión, hacemos an=f(n) para todo entero positivo n. Si consideramos una sucesión como una función f, entonces podemos considerar su grafica en un plano xy. Como el dominio de f, es el conjunto de enteros positivos, los únicos puntos de la grafica son
(1,a1),(2,a2),(3,a3),...,(n,an),...,
Otra notación para una sucesión con n-ésimo termino an es {an}; por ejemplo, la sucesión {2n} tiene como n-ésimo termino an= 2n Con la notación de sucesiones, lo escribimos de esta manera: 21,23,23,...,2n,...
Por definición, la sucesión {2n} es la función f con f(n)=2n Para todo entero positivo n.
2.8 Funciones Inversas. Logarítmicas. Trigonométricas.
FUNCIONES INVERSAS.- Son dos funciones tales que a todo punto de la gráfica
de la primera función corresponde un punto de la gráfica de la segunda, de tal
manera que la abscisa de cada punto de la primera es igual a la ordenada del
punto correspondiente de la otra y viceversa; es decir, a todo punto de la primera
curva corresponde, en la segunda, otro punto simétrico con respecto a la bisectriz
del ángulo XOY.
FUNCIONES LOGARÍTMICAS.- Una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1
FUNCIONES TRIGONOMÉTRICAS.- son las funciones que se definen a fin de extender la definición de las razones trigonométricas a todos los números reales.
surgen de una forma natural al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados sólo dependen del valor de los ángulos del triángulo.
de la primera función corresponde un punto de la gráfica de la segunda, de tal
manera que la abscisa de cada punto de la primera es igual a la ordenada del
punto correspondiente de la otra y viceversa; es decir, a todo punto de la primera
curva corresponde, en la segunda, otro punto simétrico con respecto a la bisectriz
del ángulo XOY.
FUNCIONES LOGARÍTMICAS.- Una función se llama logarítmica cuando es de la forma y = log a x donde la base a es un número real y positivo pero distinto de 1
En la función logarítmica (cuando a > 1) cuanto mayor es la base del logaritmo, más cerca del eje X está.
Las funciones de la forma y = log a x cuando la base es mayor que la unidad (a > 1) tienen las siguientes características:
(tomando como ejemplo la función f (x) = log 5 x)
-Dominio: el dominio de la función son los reales positivos puesto que no existe el logaritmo de un número negativo. Dom (f) = R +
surgen de una forma natural al estudiar el triángulo rectángulo y observar que las razones (cocientes) entre las longitudes de dos cualesquiera de sus lados sólo dependen del valor de los ángulos del triángulo.
2.7 Operaciones con funciones: adición, multiplicación, composición.

Las funciones se pueden utilizar de la misma manera que los números: sumar, restar, multiplicar, dividir, elevar a una potencia, sacar raíz o se puede hacer combinaciones.
Composicion de Funciones:
Dos funciones se combinan para producir un resultado. Por ejemplo: f actúa sobre x para producir f(x) y luego g actúa sobre f(x) o también llamada función composición que se representa g(f(x))
Defincion.- sean f, g dos funciones de variable real. Entonces se pueden definir las siguientes operaciones: Suma, Resta, Producto , Cociente.
sábado, 18 de octubre de 2014
2.6 Función definida por mas de una regla de correspondencia. Función valor absoluto.
Función definida por mas de una regla de correspondencia,- La función de valor absoluto tiene por ecuacionsiempre presenta distancias: por lo tanto, siempre sera positiva o nula.
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrara jamas debajo del eje x.
Su eje siempre va a estar por encima de dicho eje, a lo sumo tocándolo.
Las funciones en valor absoluto siempre representan una distancia o intervalos y se pueden resolver o calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto y se calculan sus raíces_(los valores de x)
2. Se forman intervalos con las raíces(los valores de x) y se evalúa el signo de cada intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la X es negativa se cambia el signo de loa función.
4. Representamos la función resultante.
Función valor absoluto.- El valor absoluto de un numero real es su valor numérico sin tener en cuenta su signo, sea este positivo o negativo. Asi por ejemplo, 3 es el valor absoluto de 3 y -3. El valor absoluto esta relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un numero real puede generalizarse a muchos otros objetos matemáticos.
En esta condición, de ser siempre positiva o nula, su gráfica no se encontrara jamas debajo del eje x.
Su eje siempre va a estar por encima de dicho eje, a lo sumo tocándolo.
Las funciones en valor absoluto siempre representan una distancia o intervalos y se pueden resolver o calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto y se calculan sus raíces_(los valores de x)
2. Se forman intervalos con las raíces(los valores de x) y se evalúa el signo de cada intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la X es negativa se cambia el signo de loa función.
4. Representamos la función resultante.
Función valor absoluto.- El valor absoluto de un numero real es su valor numérico sin tener en cuenta su signo, sea este positivo o negativo. Asi por ejemplo, 3 es el valor absoluto de 3 y -3. El valor absoluto esta relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un numero real puede generalizarse a muchos otros objetos matemáticos.
2.5 Funciones trascendentes: funciones trigonométricas, y funciones exponenciales.
Funciones trigonométricas.- Las funciones trigonométricas asocian a cada numero real, X, el valor de la razón trigonométrica del angulo cuya medida en radianes es de X.













Funciones exponenciales.-

2.4 Funciones algebraicas: función polinomial, racional e irracional.
Funciones polinomiales.- cualquier función que pueda obtenerse a partir de las funciones constantes y de la función identidad por medio del uso de las operaciones de suma, resta y multiplicación se le denomina: función polinomial.
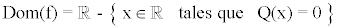
Funcion polinomial.
Función racional.- Una función es racional si el cociente de dos polinomios f(x)= P(x)
---------
Q(x)
Siendo el grado del polinomio Q(x) distinto de 0.
Las características generales de las funciones racionales son:
1) El dominio de las funciones racionales son los números reales menos las raíces del denominador, es decir:
2) Son discontinuas en los valores de x que son raíces del denominador.
3) Tienen asintotas verticales en cada raíz del denominador que no lo sea del numerador, y pueden tener asintotas horizontales y oblicuas.
Función irracional.- Las funciones irracionales son aquellas cuya expresión matemática f(x) presenta un radical: 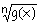
donde g (x) es una función polinomica o una función racional.
Si n es par, el radical esta definido para g(x) mayor igual a 0; así que a los efectos de calcular el dominio de f(x) que contenga un radical, habrá que imponer la condición anterior al conjunto de la expresión f(x).
2.3 Función real de variable real y su representación gráfica.
Cualquier función cuyo rango de conjunto incluya solo números reales es llamada una función " valorada real o simplemente una función real".
Si hablamos de términos matemáticos, una definición formal de una función valorada real seria " una función f: X--> Y se llama una función valorada real si asocia un único elemento del conjunto Y a cada elemento del conjunto X, donde X e Y son subconjuntos del conjunto R (conjunto de todos los números reales).
En términos simples se puede decir que una función que tiene el dominio y el co-dominio su conjunto, como subconjunto de R se llama una función real.
Un conjunto de todos los posibles pares ordenados (x, ff (x)) se le llama gráfico de una función. En caso que el conjunto que contiene X sea un conjunto de números reales; la gráfica se llama grafía de la función valorada real.
Generalmente el gráfico de tal función es una superficie, donde la entrada de la función es un par ordenado de numero s reales (x1, x2) y la salida, es decir, el gráfico formado es un triple te (z1,x2, f(x1,x2)

Si hablamos de términos matemáticos, una definición formal de una función valorada real seria " una función f: X--> Y se llama una función valorada real si asocia un único elemento del conjunto Y a cada elemento del conjunto X, donde X e Y son subconjuntos del conjunto R (conjunto de todos los números reales).
En términos simples se puede decir que una función que tiene el dominio y el co-dominio su conjunto, como subconjunto de R se llama una función real.
Un conjunto de todos los posibles pares ordenados (x, ff (x)) se le llama gráfico de una función. En caso que el conjunto que contiene X sea un conjunto de números reales; la gráfica se llama grafía de la función valorada real.
Generalmente el gráfico de tal función es una superficie, donde la entrada de la función es un par ordenado de numero s reales (x1, x2) y la salida, es decir, el gráfico formado es un triple te (z1,x2, f(x1,x2)

2.2 Función inyectiva, suprayectiva y función biyectiva.
Función inyectiva.- Una función es inyectiva si a cada valor del conjunto (dominio) le corresponde un valor distinto en el conjunto de. Es decir, a cada elemento del conjunto A le corresponde un solo valor tal que, en el conjunto A no puede haber dos o mas elementos que tengan la misma imagen.




Función Suprayectiva.- Una función es suprayectiva, si esta aplicada sobre todo el condominio, es decir, cuando la imagen, o en palabras mas sencillas, cuando cada elemento de Y es la imagen de como mínimo un elemento de X. ".

Función biyectiva.- Una función es biyectiva si al mismo tiempo inyectiva y suprayectiva.
Para ser mas claro se dice que una función es biyectivaa cuando todos los elementos del conjunto de partida en este caso (x) tienen una imagen distinta en el conjunto de llegada, que es la regla de la función inyectiva. Sumándole que cada elemento del conjunto de salida le corresponde un elemento del conjunto de llegada en este caso Y que es la norma que exige la función suprayectiva.

Explicacion sencilla.
viernes, 17 de octubre de 2014
2.1 Concepto de variable, función, dominio, contradominio y recorrido de una función.
Variable.- Es una cantidad a la que se le puede asignar diferentes valores en el proceso de un análisis. Las variables se designan usualmente con las ultimas letras del alfabeto(w,x,y,z, etc.)
Función.- Es la relación entre dos conjuntos A y B, donde el resultado de B es dependiente de A.
Dominio.- El dominio de una función esta ligado a la definición de función. Una función es una relación que asigna a cada elemento de un conjunto X uno y solo un elemento de un conjunto Y.
Al conjunto X se le llama dominio de la función y a sus elementos se les denomina también valores de entrada.
El dominio de una función es el conjunto de todos los valores de entrada que al aplicar la función llevan un valor de salida.
Contradominio.- El conjunto Y recibe el nombre de contradominio o rango de la función y son los valores de salida.La variable Y es la variable dependiente (depende de X) y se gráfica en el eje vertical, Se le considera el valor de la función. Por eso se pone: Y= f(x)
Recorrido de la función.- Son los valores que puede tomar la Y tal que se imagen de X.
Recorrido de una función; Rf: y= f(x)
Función.- Es la relación entre dos conjuntos A y B, donde el resultado de B es dependiente de A.
Dominio.- El dominio de una función esta ligado a la definición de función. Una función es una relación que asigna a cada elemento de un conjunto X uno y solo un elemento de un conjunto Y.
Al conjunto X se le llama dominio de la función y a sus elementos se les denomina también valores de entrada.
El dominio de una función es el conjunto de todos los valores de entrada que al aplicar la función llevan un valor de salida.
Contradominio.- El conjunto Y recibe el nombre de contradominio o rango de la función y son los valores de salida.La variable Y es la variable dependiente (depende de X) y se gráfica en el eje vertical, Se le considera el valor de la función. Por eso se pone: Y= f(x)
Recorrido de la función.- Son los valores que puede tomar la Y tal que se imagen de X.
Recorrido de una función; Rf: y= f(x)
Explicación sencilla.
domingo, 5 de octubre de 2014
1.6 VALOR ABSOLUTO Y SUS PROPIEDADES.
El valor absoluto de un numero entero es el numero natural que resulta al suprimir su signo.
El valor absoluto lo escribiremos entre barras y verticales.
|-5| =5
|5|=5
Propiedades:
Vídeo del valor absoluto.
El valor absoluto lo escribiremos entre barras y verticales.
|-5| =5
|5|=5
Propiedades:
Vídeo del valor absoluto.
1.4 INTERVALOS Y SU REPRESENTACIÓN MEDIANTE DESIGUALDADES.
A continuación se muestra una tabla con datos, sobre las desigualdades sus partes.
Una desigualdad es una oración matemática que contiene signo de igual, por ejemplo:
6 + 4= 10
x + 6= 10
Una igualdad que tiene variable (valor desconocido o incógnita) se llama ecuación. Por ejemplo:
Una desigualdad es una oración matemática que contiene un signo de desigualdad. Los signos de desigualdad son:
< menor que
> mayor que
≥ mayor igual que
≤ menor igual que
1.3 PROPIEDADES DE LOS NÚMEROS REALES.
Los números reales tienen algunas de las propiedades básicas de las matemáticas que por lo general pueden ser articuladas con respecto de las 2 operaciones elementales de multiplicación y suma.Algunas de estas propiedades son:
1.2 LOS NÚMEROS REALES.
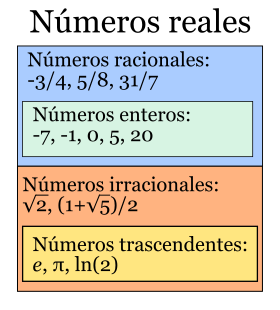
Los números reales (designados por "R") incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, transcendentales y algebraicos. El concepto de los números reales surgió a partir de la utilización de las fracciones comunes por parte de los egipcios cerca del 1,000 a.c. El desarrollo de la noción continuo con los aportes de los griegos, que proclamaron la existencia de los números irracionales.En general todos los números de uso diario, son números reales.

1.1 REPRESENTACIÓN DE LA "RECTA NUMÉRICA".
La recta numérica es un gráfico unidimensional de una linea recta en la que los números enteros son mostrados como puntos especialmente marcados que están separados uniformemente.

Esta dividida en dos mitades simétricas por el origen, es decir el numero cero, En la recta numérica, a la izquierda se encuentras los negativos (rojos) y a la derecha los positivos (azul).
En una recta numérica pueden ubicarse también las fracciones y los números irracionales.
EJEMPLO.

Esta dividida en dos mitades simétricas por el origen, es decir el numero cero, En la recta numérica, a la izquierda se encuentras los negativos (rojos) y a la derecha los positivos (azul).
EJEMPLO.
Suscribirse a:
Entradas (Atom)
 entre las variables x e y:
entre las variables x e y:












