En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de ycon respecto a x puede ser calculada con el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.
En términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si  es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 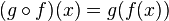 es diferenciable en
es diferenciable en  y
y
 es diferenciable en
es diferenciable en  y
y  es una función diferenciable en
es una función diferenciable en  , entonces la función compuesta
, entonces la función compuesta 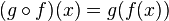 es diferenciable en
es diferenciable en  y
y
No hay comentarios:
Publicar un comentario